Question

Two spherical conductors are separated by a distance much larger than either of their radii. Sphere A has a radius of 11.5 cm and a net charge of − 95.5 nC, whereas sphere B, which is initially neutral, has a radius of 74.4 cm. The two spheres are then connected by a thin metal wire. What is the charge on sphere B after equilibrium has been reached?

Answer 1

Step-by-step explanation:

As the given spheres are connected by a thin wire so, the potential on the spheres are the same.

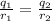`(q_(1))/(r_(1)) = (q_(2))/(r_(2))` ......... (1)

Hence, total charge will be as follows.

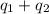`q_(1) + q_(2)` = Q = -95.5 nC .......... (2)

Using the above two equations, the final equation will be as follows.

`q_(2) = (Qr_(2))/(r_(1) + r_(2))`

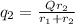
and,
`q_(1) = (Qr_(1))/(r_(1) + r_(2))`

Hence, we will calculate the charge on sphere B after the equilibrium is reached as follows.

`q_(2) = (Qr_(2))/(r_(1) + r_(2))`

=
`(-95.5 * 74.4 cm)/((11.5 + 74.4) cm)`

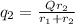
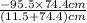
= 82.714 nC

Thus, we can conclude that the charge on sphere B after equilibrium has been reached is 82.714 nC.