Answer:
The critical value that corresponds to a confidence level of 99% is, 2.58.
Explanation:
Consider a random variable X that follows a Binomial distribution with parameters, sample size n and probability of success p.
It is provided that the distribution of proportion of random variable X,
 , can be approximated by the Normal distribution.
, can be approximated by the Normal distribution.
The mean of the distribution of proportion is,

The standard deviation of the distribution of proportion is,
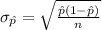 .
.
Then the confidence interval for the population proportion p is:

The confidence level is 99%.
The significance level is:
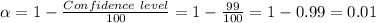
Compute the critical value as follows:
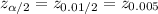
That is:

Use the z-table for the z-value.
For z = 2.58 the P (Z < z) = 0.995.
And for z = -2.58 the P (Z > z) = 0.005.
Thus, the critical value is, 2.58.