The equation of the line that passes through the points (3,1) and (6,6) is:
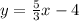
Solution:
Given that,
We have to find the equation of the line that passes through the points (3,1) and (6,6)
Find the slope of line
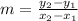
From given,
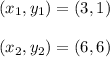
Substituting the values we get,
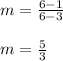
The slope intercept form of line is given as:
y = mx + c ------ eqn 1
Where,
m is the slope
c is the y intercept
Substitute m = 5/3 and (x, y) = (3, 1) in eqn 1
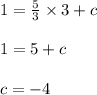
Substitute m = 5/3 and c = -4 in eqn 1
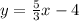
Thus the equation of line in slope intercept form is found