Question

(1 point) In a survey of 207 people, the following data were obtained relating gender to political orientation: Republican (R) Democrat (D) Libertarian (L) Total Male (M) 61 22 18 101 Femal (F) 52 42 12 106 Total 113 64 30 207 Be accurate to 4 decimal places. A person is randomly selected. What is the probability that the person is: a) Male? b) Male and a Democrat? c) Male given that the person is a Democrat? d) Republican given that the person is Male? e) Female given that the person is a Libertarian? f) Are the events Male and Republican independent? Enter yes or no . Note: You can earn partial credit on this problem.

Answer 1

(a) The probability of a person being a Male is 0.49.

(b) The probability of a person being a Male and a Democrat is 0.11.

(c) The probability of a person is a Male given that he is a Democrat is 0.35.

(d) The probability of a person is a Republican given that he is a Male is 0.61.

(e) The probability of a person is a Female given that she is a Libertarian is 0.40.

(f)

Explanation:

The given distribution of the data relating gender to political orientation is given in the tabular form below.

(a)

Compute the probability that the person is a Male as follows:

`P(Male)=(n(Male))/(N) =(101)/(207) =0.487923\approx0.49`

Thus, the probability of a person being a Male is 0.49.

(b)

Compute the probability that the person is a Male and a Democrat as follows:

`P(M\cap D)=(n(M\cap D))/(N) =(22)/(207) =0.10628\approx0.11`

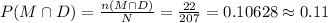
Thus, the probability of a person being a Male and a Democrat is 0.11.

(c)

Compute the probability that the person is a Male given that he is a Democrat as follows:

`P(M| D)=(P(M\cap D))/(P(D)) =(P(M\cap D))/(n(D)/ N)= (0.11)/(64/207) =0.354839\approx0.35`

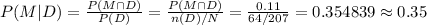
Thus, the probability of a person is a Male given that he is a Democrat is 0.35.

(d) Are the events Male and Republican independent? NO.

Compute the probability that the person is a Republican given that he is a Male as follows:

`P(R| M)=(P(R\cap M))/(P(M)) =(n(R\cap M)/N)/(P(M))= (61/207)/(0.49) =0.612245\approx0.61`

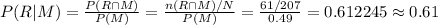
Thus, the probability of a person is a Republican given that he is a Male is 0.61.

(e)

Compute the probability that the person is a Female given that she is a Libertarian as follows:

`P(F|L)=(P(F\cap L))/(P(L)) =(n(F\cap L)/N)/(n(L)/ N)= (12/207)/(30/207) =0.40`

Thus, the probability of a person is a Female given that she is a Libertarian is 0.40.

(f)

If two event A and B are independent than their conditional probability is:

`P(B|A)=(P(A\cap B))/(P(A)) =(P(A)P(B))/(P(A))=P(B)`

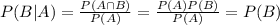
Then the conditional probability of Republican given male should be equal to the probability of Republican if the events Male and Republican independent, i.e. If the events Male and Republican independent then,

`P(R|M) = P(R)`

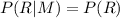
The probability of a person being a Republican is:

`P(R)= (n(R))/(N) =(113)/(207)= 0.55`

The probability of Republican given male is, P (R|M) = 0.61.

P (R|M) ≠ P (R)

Thus, the events Male and Republican are not independent.