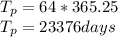Answer:
23376 days
Step-by-step explanation:
The problem can be solved using Kepler's third law of planetary motion which states that the square of the period T of a planet round the sun is directly proportional to the cube of its mean distance R from the sun.

where k is a constant.
From equation (1) we can deduce that the ratio of the square of the period of a planet to the cube of its mean distance from the sun is a constant.

Let the orbital period of the earth be
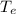 and its mean distance of from the sun be
and its mean distance of from the sun be
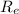 .
.
Also let the orbital period of the planet be
 and its mean distance from the sun be
and its mean distance from the sun be
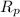 .
.
Equation (2) therefore implies the following;
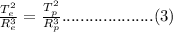
We make the period of the planet
 the subject of formula as follows;
the subject of formula as follows;
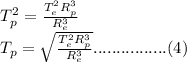
But recall that from the problem stated, the mean distance of the planet from the sun is 16 times that of the earth, so therefore
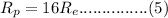
Substituting equation (5) into (4), we obtain the following;
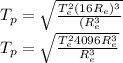
 cancels out and we are left with the following;
cancels out and we are left with the following;
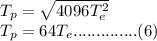
Recall that the orbital period of the earth is about 365.25 days, hence;