Question

Consider the following reaction: Fe3+(aq)+SCN−(aq)⇌FeSCN2+(aq) A solution is made containing an initial [Fe3+] of 1.2×10−3 M and an initial [SCN−] of 8.0×10−4 M . At equilibrium, [FeSCN2+]= 1.8×10−4 M .

Answer 1

The question is incomplete, here is the complete question:

Consider the following reaction:
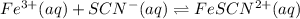`Fe^(3+)(aq)+SCN^-(aq)\rightleftharpoons FeSCN^(2+)(aq)` A solution is made containing an initial
`[Fe^(3+)]` of 1.2×10⁻³ M and an initial [SCN⁻] of 8.0×10⁻⁴ M . At equilibrium, [FeSCN²⁺]= 1.8×10⁻⁴ M.

Calculate the value of the equilibrium constant (Kc).

Answer: The value of
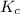`K_c` for above equation is 284.63

Step-by-step explanation:

We are given:

Initial concentration of
`[Fe^(3+)]=1.2* 10^(-3)M`

Initial concentration of
`[SCN^(-)]=8.0* 10^(-4)M`

Equilibrium concentration of
`[FeSCN^(2+)]=1.8* 10^(-4)M`

The given chemical equation follows:

`Fe^(3+)(aq)+SCN^-(aq)\rightleftharpoons FeSCN^(2+)(aq)`

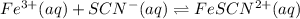
Initial:
`1.2* 10^(-3)`
`8.0* 10^(-4)`

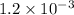
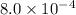
At eqllm:
`(1.2* 10^(-3)-x)`
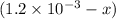
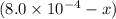`(8.0* 10^(-4)-x)` x

Equilibrium concentration of
`[Fe^(3+)]=(1.2* 10^(-3))-(1.8* 10^{-4)=1.02* 10^(-3)M`

Equilibrium concentration of
`[SCN^(-)]=(8.0* 10^(-3))-(1.8* 10^{-4)=6.2* 10^(-4)M`

The expression of
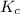`K_c` for above equation follows:

`K_c=([FeSCN^(2+)])/([Fe^(3+)][SCN^-])`

Putting values in above equation, we get:

`K_c=(1.8* 10^(-4))/((1.02* 10^(-3))* (6.2* 10^(-4)))\\\\K_c=284.63`

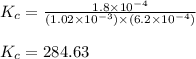
Hence, the value of
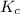`K_c` for above equation is 284.63