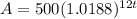Question

Alan writes the equation A=500(1.25)t to figure out how much it will cost him for a one-year loan of $500 with an interest rate of 25% compounded only once. He wants to determine the annual percentage rate (APR) for a loan that would cost the same amount overall, if it is compounded monthly, instead of only once. Which equation should he use, and what is the APR?

A≈500(1.25)12tAPR≈1.88%

A≈500(1.0188)12tAPR≈22.56%

A≈500(1.0188)12tAPR≈1.88%

A≈500(1.2512)112tAPR≈14.55%

Answer 1

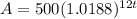`A=500(1.0188)^(12t)` , APR ≅ 22.56% ⇒ 2nd answer

Explanation:

The formula of the compounded interest is
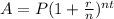`A=P(1+(r)/(n))^(nt)` , where

• A is the future value of the investment/loan, including interest
• P is the principal investment amount
• r is the annual interest rate (decimal)
• n is the number of times that interest is compounded per unit t
• t is the time the money is invested or borrowed for

∵ The equation of one-year loan of $500 with an interest rate

of 25% compounded only once is
`A=500(1.25)^(t)`

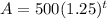
∴ t = 1

∴ A = 500(1.25) = 625

∵ A loan that would cost the same amount overall, if it is

compounded monthly, instead of only once

∴ n = 12 ⇒ compounded monthly

∵ t = 1 and n = 12

∵ P = 500

- Use the formula of the compounded interest above

∴
`A=500(1+(r)/(12))^(12)`

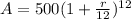
- Equate A by 625 (the value of money of the 1st equation)

∵
`500(1+(r)/(12))^(12)=625`

- Divide both sides by 500

∴
`(1+(r)/(12))^(12)=1.25`

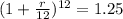
- Reverse the exponent and take it the the other side

∴
`1+(r)/(12)=(1.25)^{(1)/(12)}`

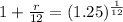
- Subtract 1 from both sides

∴
`(r)/(12)=(1.25)^{(1)/(12)}-1`

∴
`(r)/(12)=0.01876926512`

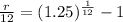
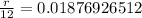
- Multiply both sides by 12

∴ r ≅ 0.2256

- Multiply it by 100%

∴ r = 22.56%

The annual percentage rate (APR) is 22.56%

Substitute the value of r in the equation above

∴
`A=500(1+(0.2256)/(12))^(12t)`

∵
`(1+(0.2256)/(12))=1.0188`

∴
`A=500(1.0188)^(12t)`

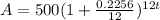
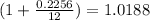
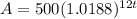
He should use the equation
`A=500(1.0188)^(12t)`