Question

A certain moving electron has a kinetic energy of 0.991 × 10−19 J. Calculate the speed necessary for the electron to have this energy. The mass of an electron is 9.109 × 10−31 kg. Answer in units of m/s.

Answer 1

4.66 × 10^5 m/s.

Step-by-step explanation:

Given:

Mass of the electron, m = 9.109 × 10^−31 kg

KE = 0.991 × 10^−19 J.

Kinetic energy, KE = 1/2 × m × v^2

v = sqrt((2 × KE)/m)

= sqrt(2.176 × 10^11)

= 4.66 × 10^5 m/s.

Answer 2

Answer: The speed necessary for the electron to have this energy is 466462 m/s

Step-by-step explanation:

Kinetic energy is the energy posessed by an object by virtue of its motion.

`K.E=(1mv^2)/(2)`

K.E= kinetic energy =
`0.991* 10^(-19)J`

m= mass of an electron =
`9.109* 10^(-31)kg`

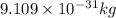
v= velocity of object = ?

Putting in the values in the equation:

`0.991* 10^(-19)J=(1* 9.109* 10^(-31)kg* v^2)/(2)`

`v=466462m/s`

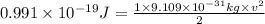
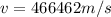
The speed necessary for the electron to have this energy is 466462 m/s