Question

Find the 6th term of the geometric sequence whose 1st term is 4 and whose common ratio is 4x3. In each of Problems 21-23, a sequence is defined recursively with a given initial condition. Use iteration to guess an explicit formula for the sequence.

Answer 1

The 6th term of the geometric sequence,
`a_(6) =4^(6)x^(15)`.

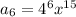Explanation:

Given,

First term (a) = 6, common ratio (r) =
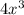`4x^3` , number of terms (n) = 6

To find, the 6th term of the geometric sequence
`(a_(6))=?`

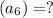
Using an explicit formula for the sequence,

The nth term of the geometric sequence,

`a_(n) =ar^(n-1)`

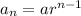
∴ The 6th term of the geometric sequence,

`a_(6) =4(4x^3)^(6-1)`

⇒
`a_(6) =4(4x^3)^(5)`

⇒
`a_(6) =4(4^5)x^(3* 5)`

⇒
`a_(6) =4^(5+1)x^(15)`

⇒
`a_(6) =4^(6)x^(15)`

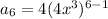
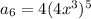
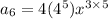
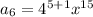
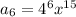
Thus, the 6th term of the geometric sequence,
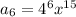`a_(6) =4^(6)x^(15)`.