Question

all a household prosperous if its income exceeds $100,000. Call the household educated if the householder completed college. Select an American household at random, and let A be the event that the selected household is prosperous and B the event that it is educated. According to a survey, P(A) = 0.137, P(B) = 0.272, and the probability that a household is both prosperous and educated is P(A and B) = 0.082. What is the conditional probability that a household is prosperous, given that it is educated? (Round your answer to four decimal places.)

Answer 1

A= the event that the selected household is prosperous

B= the event that the selected household is educated

`P(A) =0.137, P(B) =0.272, P(A \cap B) =0.082`

`P(A|B)= (0.082)/(0.272)= 0.3015`

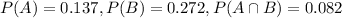
And that represent the final answer for this case.

Explanation:

For this case we define the following events:

A= the event that the selected household is prosperous

B= the event that the selected household is educated

We have the following probabilities given:

`P(A) =0.137, P(B) =0.272, P(A \cap B) =0.082`

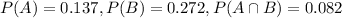
For this case we want to calculate the conditional probability that a household is prosperous, given that it is educated.

So this probability can be expressed as
`P(A|B)`

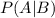
Using the Bayes rule we know that:

`P(A|B) = (P(A \cap B))/(P(B))`

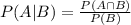
And for this case we have everything in order to replace, and we got:

`P(A|B)= (0.082)/(0.272)= 0.3015`

And that represent the final answer for this case.