Answer:
magnitude of the net force is 32.49N
and the direction of the net force is 107.91°
Step-by-step explanation:
Let the first force be F₁
Let the second force be F₂
Let the net force be F
From the question;
(a) F₁ has 17.0N in magnitude and has direction θ = 58.0° counterclockwise from +x axis. i.e
|F₁| = 17.0N
θ = 58.0°
Re-write this force in vector form as follows;
F₁ = |F₁| cos θ i + |F₁| sin θ j
F₁ = [17.0 cos 58.0°] i + [17.0 sin 58.0] j
F₁ = [17.0 x 0.5299] i + [17.0 x 0.8480] j
F₁ = [9.0083] i + [14.416] j
Put the unit as follows;
F₁ = [9.0083 N] i + [14.416 N] j
(b) F₂ is already written in vector form but can be re-written as follows;
F₂ = [-19.0N ] i + [16.5N] j
(c) The net force (F) is the algebraic sum of the two forces F₁ and F₂ as follows;
F = F₁ + F₂
Substitute the values of F₁ and F₂ into the equation above;
F = [9.0083 N] i + [14.416 N] j + [-19.0N ] i + [16.5N] j
Now, collect like terms;
F = [9.0083 N] i + [-19.0 N] i + [14.416N ] j + [16.5N] j
F = -9.9917 N i + 30.916 N j ----------------(a)
===============================================================
(a) Now let's calculate the magnitude, |F|, of the net force as follows;
|F| =

|F| =

|F| =
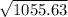
|F| = 32.49N
Therefore, the magnitude of the net force is 32.49N
(b) The direction, θ, is calculated as follows;
tan θ = (y component / x component)
tan θ = (30.916 / -9.9917)
tan θ = (-3.094)
θ = tan ⁻¹ (-3.094)
θ = -72.09°
The negative sign shows that it is measured with respect to the -x axis.
From equation (a), it is shown that the net force is located in the -i and +j directions measured counterclockwise from the +x axis. Therefore, to get the true angle of the net force relative to the positive x axis and counterclockwise, we add 180° to the angle calculated above. i.e
true angle = 180° + (-72.09°)
true angle = 107.91°
Therefore, the direction of the net force is 107.91° counterclockwise from the +x axis.