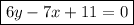Question

Find the standard equation (-1,-3)(5,4)

Answer 1

Although not specifically requested, we'll assume the question requires to find the equation of the line passing through both points

Answer:

`6y-7x+11=0`

Explanation:

Equation of a Line

To completely define the equation of a line, we only need two points through which the line passes. Let's say that our line passes through the points (x1,y1) and (x2,y2). The equation of the line can be found by

`\displaystyle y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

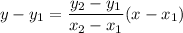
We have the coordinates of the points to be (-1,-3) and (5,4). Plugging the values into the formula:

`\displaystyle y+3=(4+3)/(5+1)(x+1)`

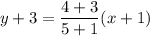
Operating

`6(y+3)=7(x+1)`

`6y+18=7x+7`

Rearranging to find the standard equation

`\boxed{6y-7x+11=0}`