Question

A geosynchronous satellite orbits Earth at a distance of 42,250 km from the center of Earth and has a period of 1 day. What is the centripetal acceleration of the satellite (in m/s2)?

Answer 1

The centripetal acceleration of the satellite is
`a=0.22\ m/s^2`.

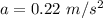Step-by-step explanation:

Given that,

The distance covered by a geosynchronous satellite, d = 42250 km

The time taken by the satellite to covered distance, t = 1 day = 24 hours

Since, 24 hours = 86400 seconds

Let v is the speed of the satellite. It is given by the total distance divided by total time taken such that :

`v=(d)/(t)`

`v=(2\pi d)/(t)`

`v=(2\pi* 42250 * 10^3)/(86400 )`

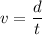
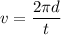
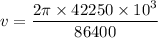
v = 3072.5 m/s

The centripetal acceleration of the satellite is given by :

`a=(v^2)/(d)`

`a=((3072.5)^2)/(42250 * 10^3)`

`a=0.22\ m/s^2`

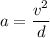
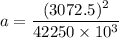
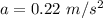
So, the centripetal acceleration of the satellite is
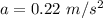`a=0.22\ m/s^2`. Hence, this is the required solution.