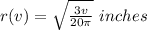Question

Which of the following functions gives the radius, r(v), of a conical artifact that is 20 inches tall as a function of its volume, v, in cubic inches?

A.

B.

C.

D.

Answer 1

Radius as function of volume is:

`r(v) = \sqrt{(3v)/(20 \pi )}\ inches`

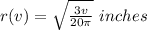
Solution:

The volume of cone is given as:

`v = (1)/(3)\pi r^(2) h`

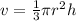
Where,

r is the radius

h is the height

From given,

height = 20 inches

From formula,

`v = (1)/(3)\pi r^(2) h`

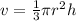
Rearrange , so that r is alone in left side of equation

`3v = \pi r^2 h\\\\\pi r^2 h = 3v\\\\r^2 = (3v)/(\pi h)\\\\Take\ square\ root\ on\ both\ sides\\\\r = \sqrt{(3v)/(\pi h)}`

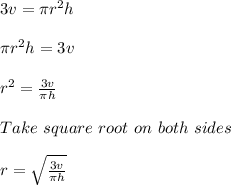
Substitute h = 20

`r = \sqrt{(3v)/(20 \pi )}`

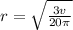
Thus, radius as function of volume is:

`r(v) = \sqrt{(3v)/(20 \pi )}\ inches`