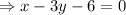Question

Write the equation of a line that is perpendicular to y=3x-2y=3x−2y, equals, 3, x, minus, 2 and that passes through the point (-9,5)(−9,5)(, minus, 9, comma, 5, ).

Answer 1

y=\purpleC{-\dfrac{1}{3}}x \greenD{+2}y=−

3

1

​

x+2

Explanation:

awd

Answer 2

Therefore the equation of required line is

x-3y-6=0

Explanation:

Line: A line can formed by joining two points. To make a line we need at least two point.

A defined portion of a line is known as line segment.

If a line passes through a point then the point will be satisfy the line.

It means (p,q) lies on a line ax+by+c=0

Then ap+bq+c=0 [putting x=p and y=q]

If two lines are perpendicular to each other then the product of their slope is -1.

Given line is

y= 3x-2.

The above equation is in form of y = mx+c

Where m is the slope of the line.

Therefore the slope of the line is = 3

Let the slope of required line be m.

Since the given line and required line perpendicular to each other.

Then,

`m* 3=-1`

`\Rightarrow m=-(1)/(3)`

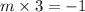
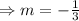
If the a line passes through a point(x₁,y₁) and slope of that line is m₁.

The equation of line is

(y-y₁)=m₁(x-x₁)

Here x₁= -9 and y₁=5

Therefore the equation of required line is

`y-5=-(1)/(3) [x-(-9)]`

`\Rightarrow 3y-15=-x-9`

`\Rightarrow x-3y-6=0`