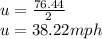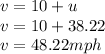Question

greg drove at a constant speed in a rainstorm for 287 miles. he took a break, and the rain stopped. he then drove 102 miles at a speed that was 10 miles per hour faster than his previous speed. If he drove for 9 hours, find the car's speed for each part of the trip

Answer 1

38.22mph and 48.22mph

Step-by-step explanation:

We first find Greg's average speed as follows. The average speed of a body is defined as the ratio of the total distance travelled by the body to the total time spent.

Total time spent, t = 9 hours

Total distance travelled, s = 287 + 102

s = 389 miles.

Hence the average speed is given thus;

`v_(avg)=(389)/(9)\\v_(avg)=43.22mph`

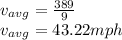
Let the speed for the first part of his journey be u and that for the last part be v, his average speed can also be expressed as follows;

`v_(avg)=(u+v)/(2)...........(1)`

Hence;

`43.22=(u+v)/(2)\\43.22*2=u+v\\86.44=u+v................(2)`

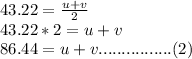
As stated in the problem, his speed for the final part of the journey was 10mph faster, therefore;

`v=10 +u....................(3)`

By substituting (3) into (2), we obtain the following;

`86.44=2u+10\\2u=86.44-10\\2u=76.44\\`

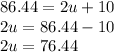
Hence,

`u=(76.44)/(2)\\u=38.22mph`

`v=10+u\\v=10+38.22\\v=48.22mph`