Answer:
correct option is b)0.16%
Explanation:
given data
defect rate P(defect ) = 3 % = 0.03
Inspectors catch = 95% = 0.95
fail nondefective = 5% = 0.05
solution
we get here P(No Defect) that is
P(No Defect) = 1 - P( Defect) .........1
P(No Defect) = 1 - 0.03
P(No Defect) = 0.97
and
P(Pass | Defect) will be
P(Pass | Defect) = 1 - Inspectors catch ...........2
P(Pass | Defect) = 1 - 0.95
P(Pass | Defect) = 0.05
and
P(Pass | No Defect) is
P(Pass | No Defect) = 1 - fail non defective ..............3
P(Pass | No Defect) = 1 - 0.05
P(Pass | No Defect) = 0.95
so now we apply here Baye's theorem
so
P(Defective | Pass) is
P(Defective | Pass) =
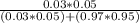
P(Defective | Pass) = 0.0016
P(Defective | Pass) = 0.16 %
so correct option is b)0.16%