Question

Logan wants to mix a17% acid solution with a 41% acid solution to get 14 L of a 36% acid solution. How many liters of the 17% solution and how many liters of the 41% solution should be mixed?

Answer 1

Answer: The volume of acid required from 17 % solution and that from 41 % solution is 2.92 L and 11.08 L respectively

Step-by-step explanation:

We are given:

Total volume of the acid solution = 14 L

Let the volume of 17 % acid solution to be added is 'x' L

So, the volume of 41 % acid solution will be = (14 - x) L

Acid solution to be made = 14 L of 36 % acid solution

Evaluating the value of 'x'

`\Rightarrow (17\% \text{ of }x)+(41\% \text{ of }(14-x))=36\%\text{ of }14\\\\\Rightarrow ((17)/(100)* x)+((41)/(100)* (14-x))=(36)/(100)* 14\\\\\Rightarrow x=2.92L`

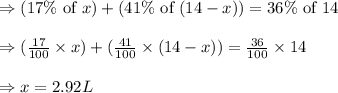
Volume of acid of 17 % solution required = x = 2.92 L

Volume of acid of 41 % solution required = (14 - x) = (14 - 2.92) L = 11.08 L

Hence, the volume of acid required from 17 % solution and that from 41 % solution is 2.92 L and 11.08 L respectively