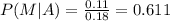Answer:
a)
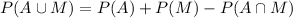
And if we solve for P(M) we got:
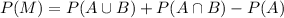
And replacing we got:
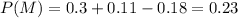
b) In order to A and M be mutually exclusive we need to satisfy:
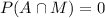
And for this case since
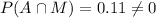 the events A and M are NOT mutually exclusive
the events A and M are NOT mutually exclusive
c) In order to satisfy independence we need to have the following relation:
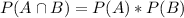
And for this case we have that:
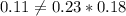
So then A and M are NOT independent
d)
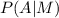
And we can use the Bayes theorem and we got:
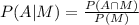
And replacing we got:

e)
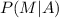
And we can use the Bayes theorem and we got:
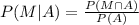
And replacing we got:
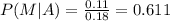
Explanation:
For this case we define the following events:
A denote the event of receiving an Athletic Scholarship.
M denote the event of receiving a Merit scholarship.
For this case we have the following probabilities given:
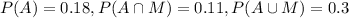
Part a
For this case we can use the total rule of probability and we have this:
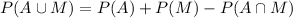
And if we solve for P(M) we got:
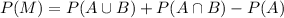
And replacing we got:
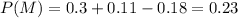
Part b
In order to A and M be mutually exclusive we need to satisfy:
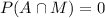
And for this case since
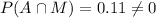 the events A and M are NOT mutually exclusive
the events A and M are NOT mutually exclusive
Part c
In order to satisfy independence we need to have the following relation:
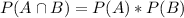
And for this case we have that:
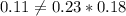
So then A and M are NOT independent
Part d
For this case we want this probability:
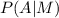
And we can use the Bayes theorem and we got:
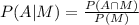
And replacing we got:

Part e
For this case we want this probability:
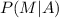
And we can use the Bayes theorem and we got:
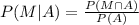
And replacing we got: