Question

Carbon disulfide has an unusual property of being able to dissolve several nonmetals. What are the boiling points and freezing points of a solution consisting of 8.44 g of P4 dissolved in 60.0 g of CS2?

Answer 1

Answer: The freezing and boiling points of the solution is -114.34°C and 48.95°C respectively

Step-by-step explanation:

• Calculating the freezing point:

Depression in freezing point is defined as the difference in the freezing point of pure solution and freezing point of solution.

The equation used to calculate depression in freezing point follows:

`\Delta T_f=\text{Freezing point of pure solution}-\text{Freezing point of solution}`

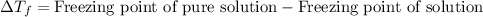
To calculate the depression in freezing point, we use the equation:

`\Delta T_f=iK_fm`

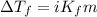
Or,

`\text{Freezing point of pure solution}-\text{Freezing point of solution}=i* K_f* \frac{m_(solute)* 1000}{M_(solute)* W_(solvent)\text{ (in grams)}}`

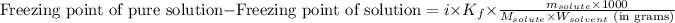
where,

Freezing point of pure solution = -110.8°C

i = Vant hoff factor = 1 (For non-electrolytes)

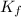`K_f` = molal freezing point constant = 3.83°C/m

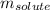`m_(solute)` = Given mass of solute
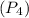`(P_4)` = 8.44 g

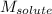`M_(solute)` = Molar mass of solute
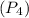`(P_4)` = 124 g/mol

`W_(solvent)` = Mass of solvent (carbon disulfide) = 60.0 g

Putting values in above equation, we get:

`-110.8-\text{Freezing point of solution}=1* 3.83^oC/m* (8.44* 1000)/(124g/mol* 60.0)\\\\\text{Freezing point of solution}=-114.34^oC`

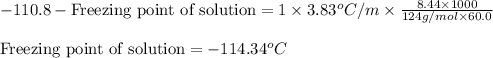
Hence, the freezing point of solution is -114.34°C

• Calculating the boiling point:

Elevation in boiling point is defined as the difference in the boiling point of solution and freezing point of pure solution.

The equation used to calculate elevation in boiling point follows:

`\Delta T_b=\text{Boiling point of solution}-\text{Boiling point of pure solution}`

To calculate the elevation in boiling point, we use the equation:

`\Delta T_b=iK_bm`

Or,

`\text{Boiling point of solution}-\text{Boiling point of pure solution}=i* K_b* \frac{m_(solute)* 1000}{M_(solute)* W_(solvent)\text{ (in grams)}}`

where,

Boiling point of pure solution = 46.3°C

i = Vant hoff factor = 1 (For non-electrolytes)

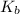`K_b` = molal boiling point constant = 2.34°C/m

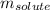`m_(solute)` = Given mass of solute
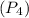`(P_4)` = 8.44 g

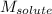`M_(solute)` = Molar mass of solute
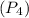`(P_4)` = 124 g/mol

`W_(solvent)` = Mass of solvent (carbon disulfide) = 60.0 g

Putting values in above equation, we get:

`\text{Boiling point of solution}-46.3=1* 2.34^oC/m* (8.44* 1000)/(124g/mol* 60.0)\\\\\text{Boiling point of solution}=48.95^oC`

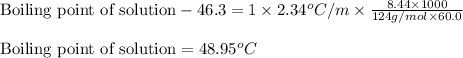
Hence, the boiling point of solution is 48.95°C