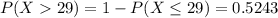Answer:
a)
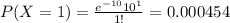
b) For this case the new parameter
 would be:
would be:
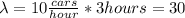
And we want to calculate the following probability:

And we can use the complement rule for this case:
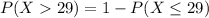
And for this case we can use the following excel code in order to find the required probability:
"=1-POISSON.DIST(29,30,TRUE)"
And we got:
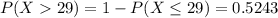
Explanation:
Part a
Let X the random variable that represent the number of cars arriving for gasoline at Shell station. We know that

The probability mass function for the random variable is given by:
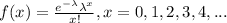
And for this case we want this probability:

Using the probability mass function we got:
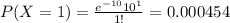
Part b
For this case the new parameter
 would be:
would be:
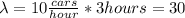
And we want to calculate the following probability:

And we can use the complement rule for this case:
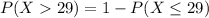
And for this case we can use the following excel code in order to find the required probability:
"=1-POISSON.DIST(29,30,TRUE)"
And we got: