y + 9 = 10(x - 6) is the point-slope form of the equation of the line that passes through the points (6, -9) and (7, 1)
Solution:
Given points are:
(6, -9) and (7, 1)
Let us find the slope of line
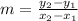
From given,
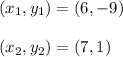
Therefore,

Thus slope of line is 10
The point slope form of line is given as:

Substitute m = 10 and
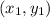 = (6, -9) in above
= (6, -9) in above
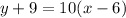
Thus the equation of line in point slope form is found