Question

A car travels around an unbanked 50 m radius curve without skidding. The coefficient of friction between the tires and road is 0.5. What is the car’s maximum speed?

Answer 1

15.81m/s

Step-by-step explanation:

In this scenario, frictional force will be acting opposite to the direction of the car and will also keep the car from skidding. And because this is the only horizontal force acting on the car, the centripetal force (F) is the frictional force (
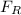`F_(R)`) itself. i.e

F =
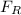`F_(R)` ----------------(i)

But we know that;

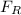`F_(R)` = μ x N

Where;

μ = coefficient of friction between the tires and the road

N = normal reaction due to the weight (m x g) of the car. [m = mass of the car and g = acceleration due to gravity = 10m/s²]

=>
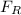`F_(R)` = μ x m x g

Also,

The centripetal force (F) is given as the product of the mass (m) of the body (car), the square of the linear speed (v) of the car and the inverse of the radius (r) of the motion path. i.e

F = m v² / r

Substitute the values of F and
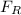`F_(R)` into equation (i) as follows;

mv²/ r = μ x m x g

Divide both sides by m;

v²/ r = μ x g -----------------------(ii)

From the question;

r = 50m

μ = 0.5

Substitute these values into equation (ii) as follows;

v²/ 50 = 0.5 x 10

v²/ 50 = 5

v² = 250

v =
`√(250)`

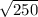
v = 15.81m/s

Therefore, the maximum speed of the car is 15.81m/s

Answer 2

V = 15.66 m/s

Step-by-step explanation:

In this satiation Fnet = F (centripetal) = f (Horizontal)

⇒ mV²/r = μ mg

⇒V = Square Root (μgr)

V = 15.66 m/s