Answer:
The value of the quantity after 144 hours is 19,200.
Explanation:
Let the quantity to be found be P(t) where t is the time in hours
Let
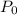 be the initial amount. Therefore
be the initial amount. Therefore
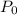 = 2400.
= 2400.
The amount doubles every 2 days. The equivalent of 2 days is 48 hours
So the equation that can model the given data will be given by
P(t) =
 where t is the time in hours.
where t is the time in hours.
We divide the time t by 48 to find out how many time does the quantity actually double.
Therefore the value of the quantity after 144 hours is ,
P(144) = 2400 ×
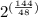 =
=
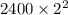 = 2400 × 8 = 19200.
= 2400 × 8 = 19200.