Complete Question:
A mass resting on a horizontal, frictionless surface is attached to one end of a spring; the other end is fixed to a wall. It takes 3.6 J of work to compress the spring by 0.13 m. If the spring is compressed, and the mass is released from rest, it experiences a maximum acceleration of 12m/s². Find the value of
(a) the spring constant and
(b) the mass.
Giancoli, Douglas C.. Physics (p. 323). Pearson Education. Kindle Edition.
Answer:
(a) 426.04N/m
(b) 4.62kg
Step-by-step explanation:
(a) According to Hooke's law, work done is stored as the potential energy (E) due to the compression of the spring is given by;
E =
 x k x e² ----------------------(i)
x k x e² ----------------------(i)
Where;
k = the spring constant of the spring
e = the compression
According to the question;
e = 0.13m
E = 3.6J
Substitute these values into equation (i) as follows;
3.6 =
 x k x 0.13²
x k x 0.13²
3.6 =
 x k x 0.0169
x k x 0.0169
3.6 = k x 0.00845
Now solve for k;
k = 3.6 / 0.00845
k = 426.04 N/m
Therefore, the spring constant is 426.04N/m
(b) When the spring is compressed and the mass is released from rest, the same force (F) on the spring will cause the mass to accelerate. i.e
F = k x e -----------Force on spring [From Hooke's law]
F = m x a ----------Force causing the acceleration(a) [From Newton's law]
Combine the two equations as follows;
k x e = m x a -------------------(ii)
Where a = 12m/s², substitute the other necessary values into equation (ii) as follows;
426.04 x 0.13 = m x 12
55.385 = 12m
Solve for m as follows;
m =
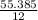
m = 4.62kg
Therefore, the mass is 4.62kg