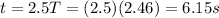Answer:
6.15 s
Step-by-step explanation:
The period of a simple pendulum is given by the equation
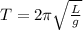
where
L is the length of the pendulum
g is the acceleration of gravity
For the pendulum in this problem,
L = 1.5 m (length)
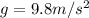 (acceleration due to gravity on Earth)
(acceleration due to gravity on Earth)
Therefore, its period is
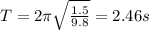
And therefore, the time taken for the pendulum to complete 2.5 oscillations is equal to 2.5 times the period: