Question

Pls answer thank you

Answer 1

Option A :
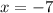`$x=-7$` is the equation of the vertical asymptote

Option D :
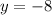`y=-8` is the equation of the horizontal asymptote

Step-by-step explanation:

The given function is
`$f(x)=(5)/(x+7)-8$`

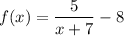
The vertical asymptote of the function can be determined by equating the numerator to zero.

Thus, we have,

`x+7=0`

`x=-7`

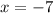
Thus, the vertical asymptote of the function is
`x=-7`

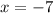
Hence, Option A is the correct answer.

Now, we shall determine the horizontal asymptote of the function.

If
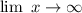`$\lim\ {x \rightarrow \infty}`, then the function
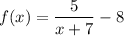`$f(x)=(5)/(x+7)-8$` becomes,

`$\lim _(x \rightarrow \infty) f(x)=\lim _(x \rightarrow \infty) (5)/(x+7)-8=-8`

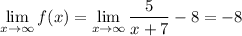
Thus, the horizontal asymptote of the function is
`y=-8`

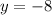
Hence, Option D is the correct answer.