Answer:
99 percent confidence interval for the true mean is [11.28 , 33.63] .
Explanation:
We are given that there is an average of 22.455 employees at 22 office furniture dealers in a major metropolitan area, with a standard deviation of 18.52.
The Pivotal quantity for 99% confidence interval is given by;
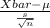 ~
~

where, X bar = sample mean = 22.455
s = sample standard deviation = 18.52
n = sample size = 22
So, 99% confidence interval for the true mean number of full-time employees at office furniture dealers,
 is given by;
is given by;
P(-2.831 <
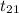 < 2.831) = 0.99
< 2.831) = 0.99
P(-2.831 <
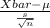 < 2.831) = 0.99
< 2.831) = 0.99
P(-2.831 *
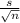 <
<
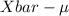 < 2.831 *
< 2.831 *
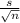 ) = 0.99
) = 0.99
P(X bar - 2.831 *
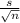 <
<
 < X bar + 2.831 *
< X bar + 2.831 *
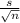 ) = 0.99
) = 0.99
99% confidence interval for
 = [ X bar - 2.831 *
= [ X bar - 2.831 *
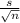 , X bar + 2.831 *
, X bar + 2.831 *
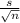 ]
]
= [ 22.455 - 2.831 *
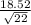 , 22.455 + 2.831 *
, 22.455 + 2.831 *
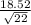 ]
]
= [11.28 , 33.63]
Therefore, 99 percent confidence interval for the true mean number of full-time employees at office furniture dealers is [11.28 , 33.63] .