Answer:
a) The doubling time is 7.27 hours.
b) The population is 6 hours will be 3,543.
Explanation:
The population of the bacteria is modeled by the following equation:

In which P(0) is the initial population, P(t) is the population after t hours and r is the growth rate.
An experiment starts and the population of a bacteria culture increases by 10% in the first hour.
This means that
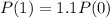
Which helps us find r.
So


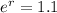
Applying ln to both sides
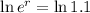
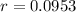
So

a) What is the doubling time?
This is t when
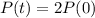
So


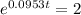
Applying ln to both sides
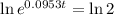
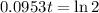
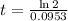
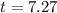
The doubling time is 7.27 hours.
b) If the initial population is 2,000, what is the population in 6 hours?
This is P(6) when
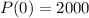 . So
. So

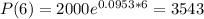
The population is 6 hours will be 3,543.