Question

What is the equation of the line passing through the points  (Two-fifths, StartFraction 19 Over 20 EndFraction)and  (one-third, StartFraction 11 Over 12 EndFraction) in slope-intercept form?​

Answer 1

THe answer is B

Explanation:

Answer 2

4x - 8y = -6 is the equation of line in standard form

Solution:

The equation of line in point slope form is given as:

`y - y_1 = m(x-x_1)`

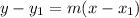
Where, m is the slope of line

The slope of line is given as:

`m = (y_2-y_1)/(x_2-x_1)`

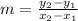
From given,

`(x_1, y_1) = ((2)/(5) , (19)/(20))\\\\(x_2, y_2) = ((1)/(3) , (11)/(12))`

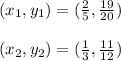
Substituting the values we get,

`m = ((11)/(12) - (19)/(20))/((1)/(3) - (2)/(5))\\\\Simplify\\\\m = (-8)/(240) * (15)/(-1)\\\\ m = (120)/(240)\\\\m = (1)/(2)`

`\text{Substitute } m = (1)/(2) \text{ and } (x_1, y_1) = ((2)/(5) , (19)/(20)) \text{ in eqn 1 }`

`y - (19)/(20) = (1)/(2)(x - (2)/(5))\\\\y - (19)/(20) = (x)/(2) - (1)/(5)\\\\(x)/(2) - y = - (19)/(20) + (1)/(5)\\\\(x)/(2) - y = (-15)/(20)\\\\Simplify\\\\y = (1)/(2)x + (3)/(4)`

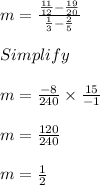
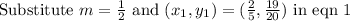
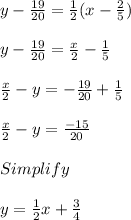
In standard form,

`y = (4x+6)/(8)\\\\8y = 4x + 6\\\\4x - 8y = -6`

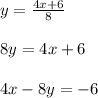
Thus the equation of line is found