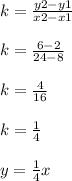Answer:
5)
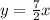
6)
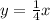
Explanation:
k in this equation represents the slope of the line. To find the slope of a line, pick 2 points that land perfectly on the grid and find the vertical and horizontal distance between them. The vertical distance is the 'rise', and the horizontal distance is the 'run'. Given those two numbers, you can calculate the slope:
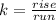
A more precise definition is:

5)
You can use whichever 2 points you want here. I'll use the 2 outermost points:
(x1, y1) = (2, 7)
(x2, y2) = (8, 28)
Now, to find the distance between them, subtract the position of the first point from the second point. Vertical distance first, subtract the y-coordinates:

The rise is 21.
Horizontal distance, subtract the x-coordinates:
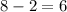
Slope is 'rise over run' as I wrote above, so you can now write the slope and the equation of the line:
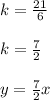
6)
I'll pick the 2 outermost points again:
(x1, y1) = (8, 2)
(x2, y2) = (24, 6)
This time, I'll just plug all 4 values directly into the 2nd formula I wrote at the top.