Option C: The solution set is
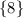
Step-by-step explanation:
The expression is
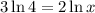
Now, let us find the solution set.
Switch sides, we get,
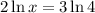
Dividing by 2 on both sides, we have,
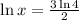
Thus,
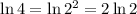
Hence, the above expression becomes,
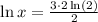
Simplifying, we get,
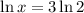
Applying the log rule, we get,
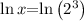
Simplifying, we have,
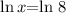
Applying the log rule, we have,
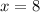
Thus, the solution set is
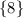
Hence, Option C is the correct answer.