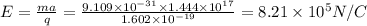Question

The electrons move with a velocity of 3.8 ×107 m/s. What electric field strength is needed to accelerate electrons from rest to this velocity in a distance of 5.0 mm?

Answer 1

Missing part of question

The electron beam inside an old television picture tube is 0.40 mm in diameter and carries a current of 50 μA. This electron beam impinges on the inside of the picture tube screen. 1-The electrons move with a velocity of 3.8 ×107 m/s. What electric field strength is needed to accelerate electrons from rest to this velocity in a distance of 5.0 mm?

Answer:

`8.21* 10^(5) N/C`

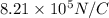
Step-by-step explanation:

From kinematics we know that

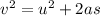`v^(2)=u^(2)+2as` where v and u are final and initial velocities respectively, s is the distance covered, a is acceleration.

We know that initial velocity is zero hence

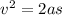`v^(2)=2as` and making a the subject then

`a=\frac {v^(2)}{2s}=\frac {(3.8* 10^(7))^(2)}{2* 5* 10^(-3)}`

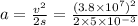
From Newton’s law, F=ma and also qE=ma hence
`E=\frac {ma}{q}=\frac {9.109* 10^(-31)* 1.444* 10^(17)}{1.602* 10^(-19)}=8.21* 10^(5) N/C`