Answer:
155 ways are there to select the committee that has more women than men.
Explanation:
The order is not important.
For examle, a committee of John, Elisa, Josh and Rose is the same committee as Elisa, John, Josh and Rose. So we use the combinations formula to solve this problem.
Combinations formula:
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

How many ways are there to select the committee that has more women than men?
It can either be 3 women and a men, or 4 women.
3 women and a men
1 men from a set of 15
3 women from a set of 5

4 women
4 women from a set of 5
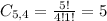
Total
150 + 5 = 155
155 ways are there to select the committee that has more women than men.