$4000 was invested at 3% interest.
Solution:
Assume that x and y represent the amount at 3.5% and 3% respectively. So, according to the given statements we get two equations,

On multiplying equation (1) by 30 and equation (2) by 10 we get,
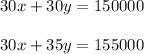
On solving both the equations we get,
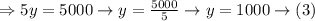
On substituting (3) in (1) we get,

Therefore, $4000 was invested at 3% interest and $1000 was invested at 3.5% interest.