Question

Find the greatest common factor: 12ab^2c^4 + 20a^4bc^3 + 16a^3b

A. 4ab
B. 4abc C. 12a^2b^2c^2 D. 20a^4b^2c^3

Answer 1

Option A

The greatest common factor is 4ab

Solution:

Given that,

We have to find the greatest common factor

`12ab^2c^4+20a^4bc^3+16a^3b`

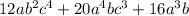
First find the GCF of numbers

GCF of 12, 20, 16

The factors of 12 are: 1, 2, 3, 4, 6, 12

The factors of 16 are: 1, 2, 4, 8, 16

The factors of 20 are: 1, 2, 4, 5, 10, 20

Then the greatest common factor is 4

Now find the GCF of variables

`ab^2c^4\\\\a^4bc^3\\\\a^3b`

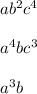
Here,

ab is the greatest common factor

Therefore, GCF of variables is ab

Thus, GCF of given expression is: 4ab