Question

A 0.67 V potential difference is maintained across a 1.2 m length of tungsten wire that has a cross-sectional area of 0.45 mm2 . What is the current in the wire? The resistivity of the tungsten is 5.6 × 10−8 Ω · m . Answer in units of A.

Answer 1

To solve this problem we will apply the concepts related to Ohm's law, described as the equivalence between the voltage and the product between the current and the resistance. At the same time we will use the concept related to the electrical resistance as a function of the characteristics of the wire to finally find the current.

Ohm's law given by the following expression

`V= IR`

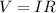
The electrical resistance of a wire would be,

`R = (\rho l)/(A)`

Here,

`\rho` = Resistivity of the material

l = Length

A = Cross-sectional area,

Replacing the value of the Resistance and Ohm's equation we have,

`R = I (\rho l)/(A)`

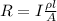
Now rearranging to find the current

`I = (VA)/(\rho l)`

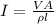
Our values are given as,

`V = 0.670V`

`l = 1.20m`

`A = 0.450mm^2`

`\rho = 5.6*10^(-8) \Omega \cdot m`

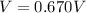
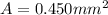
Replacing,

`I = ((0.670V)(0.450mm^2((1m)/(10^3mm))^2))/((5.6*10^(-8)\Omega \cdot m)(1.20m))`

`I = 4.4866A`

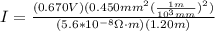
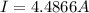
Therefore the current in the tungsten wire is 4.4866A