Question

7 measured data points have a sample mean of 1403 and a standard deviation of 27. Determine the best estimate of the mean value at 95% probability level. Find a, where the best estimate of the mean value is expected to fall ±a about the sample mean.

Answer 1

Explanation:

Hello!

You have sample of n=7 with mean X[bar]= 1403 and standard deviation S=27 and are required to estimate the mean with a 95%CI.

Asuming this sample comes from a normal population I'll use a stuent t to estimate the interval (a sample of 7 units is too small for the standard normal to be accurate for the estimation):

[X[bar]±
`t_(n-1;1-\alpha /2)` *
`(S)/(√(n) )`]

`t_(n-1;1-\alpha /2) = t_(6;0.975)= 2.365`

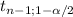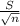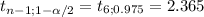
[1403±2.365*
`(27)/(√(7) )`]

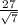[1378.87;1427.13]

The margin of error is the semiamplitude of the interval and you can calculate it as:

`d= (Upbond-Lowbond)/(2)= (1427.13-1378.87)/(2) = 24.13`

With a confidence level of 95% you'd expect that the real value of the mean is contained by the interval [1378.87;1427.13], the best estimate of the mean value is expected to be ± 24.13 of 1403.

I hope it helps!