Question

A gas tank storage has a volume of 35 L when the temperature is 27c and the the pressure is 1atm what is the new volume of the tank if the temperature drops to -10c

Answer 1

Final volume: 35 L, final pressure: 0.88 atm

Step-by-step explanation:

I assume there is a typo in the question: the volume of the gas tank is constant, so the question is "what is the new pressure in the tank?"

Since the volume of the gas is constant, we can use the pressure's law, which states that:

"For an ideal gas kept at constant volume, the pressure of the gas is proportional to its absolute temperature"

Mathematically:

`(p)/(T)=const.`

where

p is the gas pressure

T is the absolute temperature

The equation can be rewritten as

`(p_1)/(T_1)=(p_2)/(T_2)`

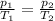
where in this problem:

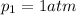`p_1=1 atm` is the initial pressure

`T_1=27^(\circ)C+273=300 K` is the initial temperature

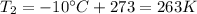`T_2=-10^(\circ)C+273=263 K` is the final temperature

Therefore, the new pressure is

`p_2=(p_1 T_2)/(T_1)=((1)(263))/(300)=0.88 atm`

While the final volume is still 35 L.