Question

A triangle with vertices at A(20, –30), B(10, –15), and C(5, –20) has been dilated with a center of dilation at the origin. The image of B, point B prime, has the coordinates (2, –3). What is the scale factor of the dilation? StartFraction 1 Over 10 EndFraction One-fifth 5 10

Answer 1

Answer: 1/5

Explanation:

Answer 2

One-fifth

Explanation:

step 1

Find the distance between the origin and the point B

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

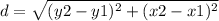
we have

O (0,0) and B(10, –15)

substitute

`d=\sqrt{(-15-0)^(2)+(10-0)^(2)}`

`d=√(325)\ units`

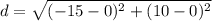
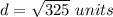
step 2

Find the distance between the origin and the point B'

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

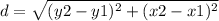
we have

O (0,0) and B'(2,-3)

substitute

`d=\sqrt{(-3-0)^(2)+(2-0)^(2)}`

`d=√(13)\ units`

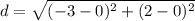
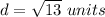
step 3

Find the scale factor of the dilation

The scale factor is equal to divide the length of segment OB' by the length of segment OB

so

`(√(13))/(√(325))=(1)/(5)`

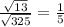
so

One-fifth