Question

Find any domain restrictions on the given rational equation

Select all that apply

A:X=3
B:X=-4
C:X=4
D:X=0

Answer 1

-4 and 3

Explanation:

Answer 2

A:x=3

B:x=-4

Explanation:

The domain is set of all values of x for which the given rational function is defined.

The rational equation is

`(50)/(4x - 12) + \frac{x - 4}{ {x}^(2) + x - 12 } = (x)/(2)`

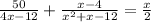
The rational function will not be defined if the denominator is zero.

That is if:

1.

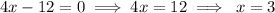
`4x - 12 = 0 \implies 4x = 12\implies \: x = 3`

2.

`{x}^(2) + x - 12 = 0\implies (x - 3)(x + 4)`

This implies that x=3 or x =-4

Therefore the equation is defined on all real values of x, except x=3 or-4