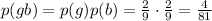Answer:
4/81
Explanation:
The candies in the packet are:
r = 5 (number of red candies)
g = 2 (number of green candies)
b = 2 (number of blue candies)
The total number of candies in the packet at the beginning is:
n = r + g + b = 5 + 2 +2 = 9
Therefore, at the first attempt, the probability of drawing a green candy is:
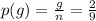
Then, the first candy is placed back in the packet, so still
n = 9
Therefore, at the second attempt, the probability of drawing a blue candy is

Therefore, the probability that a random drawing yields a green followed by a blue is: