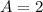Part a: The value of R when
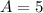 is
is
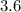
Part b: The value of A when
 is
is

Step-by-step explanation:
It is given that R is inversely proportional to A.
Hence, it can be written as
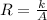
Also, it is given that
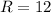 and
and
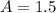
Substituting these values in
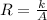 , we have,
, we have,
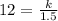
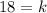
Thus, the value of K is
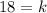
Part a: To determine the value of R when
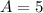
Now, substituting
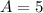 and
and
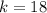 in
in
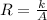 , we get,
, we get,

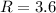
Thus, the value of R is
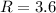
Part b: To determine the value of A when

Now, substituting
 and
and
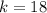 in
in
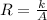 , we get,
, we get,
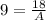
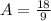
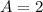
Thus, the value of A is