Question

Mortgage: $95,000; Years: 30; Interest Rate: 6%.

a. Find the monthly payment using the table above.

b. Find the total amount paid.

c. Find the total interest paid.

d. Find the monthly payment to the nearest cent using the formula above. Do not round until your final answer.

e. What is the difference (in dollars) in interest if you use the formula versus the table?

Answer 1

a. Find the monthly payment using the table above.

• $570.

b. Find the total amount paid.

• $205,200.

c. Find the total interest paid.

• $110,200

d. Find the monthly payment to the nearest cent using the formula above. Do not round until your final answer.

• $569.57

e. What is the difference (in dollars) in interest if you use the formula versus the table?

• $154.80

Step-by-step explanation:

Data:

• Mortgage: $95,000;
• Years: 30; Interest
• Rate: 6%.

a. Find the monthly payment using the table above.

Locate the cell at the intersection of the column for 30 length of loan in years, and the row for 6.00% interest.

The cell has value 6.00

That is the monthly payment for a loan of $1,000.

For a mortage of $95,000 divide by 1,000 and multiply by the value of the corresponding cell, 6.00 in this case.

• $95,000/1,000 × 6.00 = $570

Thus, the monthly payment is $570.

b. Find the total amount paid.

You need to multiply the montly payment by the number of months in 30 years.

• Number months = 12 × 30 = 360

• Total amount paid = number of months × montly payment = 360months × $570/month = $205,200

Hence, the total amount paid is $205,200.

c. Find the total interest paid.

The total interest paid is the difference between the total amount paid and tha amount of the loan (mortgage).

• Total interest = total amount paid - loan amount

• Total interest = $205,200 - $95,000 = $110,200

Therefore, the total interest pais is $110,200,

d. Find the monthly payment to the nearest cent using the formula above. Do not round until your final answer.

The formula for the factor is:

`Factor=(i(1+i)^n)/((1+i)^n-1)`

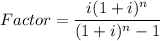
Where,

• n is the number of periods; months in this case = 360, and

• i is the interest of one period: 6%/12 = 0.06/12 = 0.005

Substitute and compute:

`Factor=(i(1+0.005)^(360))/((1+0.005)^(360)-1)=0.0059955`

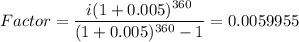
That factor is for $1.00

Multiply by $95,000:

• Payment = $95,000 × 0.00059955 = $569.57

Therefore, the monthly payment to the nearest cent using the formula is $569.57

e. What is the difference (in dollars) in interest if you use the formula versus the table?

• Total amount paid = number of payments × monthly payment

• Total amount paid = 360 months × $569.57/month = $205,045.20

• Total interest = total amount paid - amout of the loan

• $205,045.20 - $95,000 = $110,045.20

• Difference: $110,200 - $110,045.20 = $154.80

Hence, the difference in interest if you use the formula versus the table is $154.80