The general equation for the circle that passes through the points (1, 1), (1, 3), and (9, 2) is:
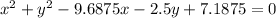
Solution:
Given that,
Write the general equation for the circle that passes through the points (1, 1), (1, 3), and (9, 2)
The general equation of the circle is of the form:
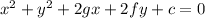
The circle passes through the point (1, 1)
Replacing x = 1 and y = 1 must satisfy the equation.
Using these values, we get:
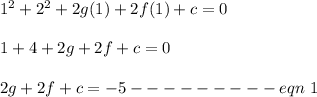
The circle passes through the point (1, 3)
Replacing x = 1 and y = 3 must satisfy the equation
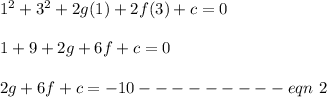
The circle passes through the point (9, 2)
Replacing x = 9 and y = 2 must satisfy the equation
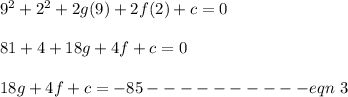
Solving eqn 1, 2, 3 using elimination, we get,
g = -4.84375
f = -1.25
c = 7.1875
Thus the general equation for the circle is:
Substitute the g, f, c values in general equation
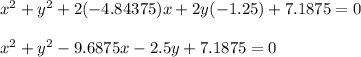
Thus the general equation for the circle is found