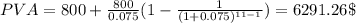Question

Plimpton has an annuity due that pays​ $800 per year for 11 years. What is the present value of the cash flows if they are discounted at an annual rate of​ 7.50%?

Answer 1

6291.26$

Step-by-step explanation:

In order to calculate the present value of the cash flow, we apply the formula for the present value of annuity due:

`PVA=P+(P)/(r)(1-(1)/((1+r)^(n-1)))`

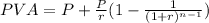
where:

P is the value of the periodic payment

r is the discout rate

n is the number of periods

In this problem, we have:

`P=\$800` (periodic payment)

n = 11 y (number of years)

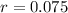`r=0.075` (discount rate is 7.5%)

Therefore, the present value of the cash flow is:

`PVA=800+(800)/(0.075)(1-(1)/((1+0.075)^(11-1)))=6291.26\$`