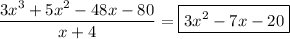Question

3x^3+5x^2-48x-80 divided by x+4

Answer 1

One way to do is to write the first polynomial in terms of the second; this means find
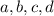`a,b,c,d` so that

`3x^3+5x^2-48x-80=a(x+4)^3+b(x+4)^2+c(x+4)+d`

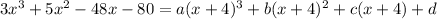
Expanding the right side and matching up coefficients of terms with the same power of
`x` gives

`\begin{cases}a=3\\12a+b=5\\48a+8b+c=-48\\64a+16b+4c+d=-80\end{cases}\implies a=3,b=-31,c=56,d=0`

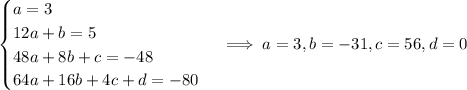
So we have

`3x^3+5x^2-48x-80=3(x+4)^3-31(x+4)^2+56(x+4)`

and in particular we can see
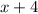`x+4` divides this exactly, giving us

`(3x^3+5x^2-48x-80)/(x+4)=3(x+4)^2-31(x+4)+56`

and expanding gives

`(3x^3+5x^2-48x-80)/(x+4)=\boxed{3x^2-7x-20}`