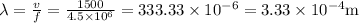Question

Diagnostic ultrasound of frequency 4.50 MHz is used to examine tumors in soft tissue. (a) What is the wavelength in air of such a sound wave? (b) If the speed of sound in tissue is 1500 m/s, what is the wavelength of this wave in tissue?

Answer 1

(a)
`7.62 * 10^(-5) m` is the wavelength in air of such a sound wave.

(b)
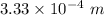`3.33 * 10^(-4)\ m` is the wavelength of this wave in tissue.

Step-by-step explanation:

Frequency and wavelength can be related by the equation,

Velocity = Wavelength x Frequency

`v=\lambda * f`

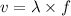
where,

v - velocity of light for all EM (electromagnetic) waves in vacuum

Given:

f - 4.50 MHz =
`4.50 * 10^(6) \mathrm{Hz}`

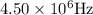
a) To find the wavelength in air

We know,

Speed of sound in air = 343 m/s

Apply given frequency and speed of sound in air, we get

`\lambda=(v)/(f)=(343)/(4.5 * 10^(6))=76.2 * 10^(-6)=7.62 * 10^(-5)\ \mathrm{m}`

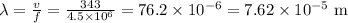
b) If the speed of sound in tissue is 1500 m/s, find the wavelength of this wave in tissue

Speed of sound in tissue, v = 1500 m/s

`\lambda=(v)/(f)=(1500)/(4.5 * 10^(6))=333.33 * 10^(-6)=3.33 * 10^(-4) \mathrm{m}`