Question

Consider an electron placed in a region of space in which the electric potential spatially. The electron is placed at a point where the potential is -1000V relative to ground, and it is observed to accelerate to a point where the potential is -500V relative to ground. How fast is the electron moving at that point, assuming nothing else impacts the electron's motion

Answer 1

`1.33\cdot 10^7 m/s`

Step-by-step explanation:

For a charged particle accelerated by an electric field, the kinetic energy gained by the particle is equal to the decrease in electric potential energy of the particle; therefore:

`K_f-K_i = -q\Delta V`

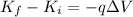
where

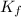`K_f` is the final kinetic energy

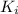`K_i` is the initial kinetic energy

q is the charge of the particle

`\Delta V` is the potential difference

In this problem,

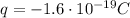`q=-1.6\cdot 10^(-19)C` is the charge of the electron

`\Delta V=-500 V-(-1000 V)=500 V`

The electron starts from rest, so its initial kinetic energy is

`K_i=0`

Therefore,

`K_f=-(-1.6\cdot 10^(-19))(500)=8\cdot 10^(-17)J`

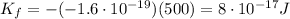
We can write the final kinetic energy of the electron as

`K_f=(1)/(2)mv^2`

where

`m=9.11\cdot 10^(-31) kg` is the electron mass

v is the final speed

And solving for v,

`v=\sqrt{(2K_f)/(m)}=\sqrt{(2(8\cdot 10^(-17)))/(9.11\cdot 10^(-31))}=1.33\cdot 10^7 m/s`