Question

All County Insurance, Inc. promises to pay Ted $1 million on his 65th birthday in return for a one-time payment of $75,000 today. (Ted just turned 25.) At what rate of interest would Ted be indifferent between accepting the company's offer and investing the premium on his own

Answer 1

`\large\boxed{\arge\boxed{6.49\%}}`

Step-by-step explanation:

The rate of interest at which Ted would be indifferent between accepting the company's offer and investing the premium on his own is the rate that makes the future value of his investment ($75,000) today equal to the value paid on his 65th birthday ($1 millon).

To calculate the future value, you must use monthly compound interest. The number of years of the investment is 65 - 25 = 40.

Thus, the number of periods is 40 years × 12 period/year = 480 periods.

The, your formula is:

`\$ 75,000(1+r)^(480)=\$ 1,000,000\\\\(1+r)^(480)=13.\overline 3`

`1+r=(13.\overline 3)^((1/480))`

`1+r=1.00541\\\\r=0.00541`

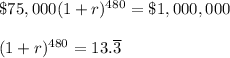
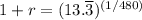
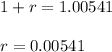
That is monthly; convert it to annual rate:

`r=0.00541* 12=0.0649`

Finally, pass to percet:

`r=0.0649* 100\% =6.49\%`